Тесты – Метод координат 9 класс с ответами: бесплатные материалы для тестирования от преподавателя.
Тесты по алгебре 9 класс. Тема: “Метод координат”
Правильный вариант ответа отмечен знаком +
1. Две перпендикулярные координатные прямые с общим началом координат в точке O называются:
– пересекающимися хордами
– векторной плоскостью
+ прямоугольной системой координат
– диагоналями параллелограмма
2. Что такое координатная плоскость?
– плоскость, которую можно представить при помощи нескольких координатных четвертей
+ плоскость с заданной прямоугольной системой координат
– плоскость, которая соединяет любые точки прямой
– плоскость, которая имеет начало координат
3. Как иначе называется прямоугольная система координат?
– Эвклидова
+ Декартова
– Пифагорова
– Лагранжева
4. Как называются участки прямоугольной системы координат, образованные пересечением двух осей?
– сектора
– квадранты
– кластеры
+ четверти
5. Как называют координатные прямые на координатной плоскости?
– ось Z и ось Y
– перпендикулярные прямые
+ ось абсцисс и ось ординат
– диагонали координатной плоскости
6. Если из точки S, расположенной на координатной плоскости, опустить прямую, перпендикулярную оси x, то координата точки пересечения этой прямой с осью Ox, называется:
– началом координат
+ абсциссой точки S
– ординатой точки S
– модулем точки S
7. Сколько существует абсцисс и ординат для точки, расположенной во второй четверти прямоугольной системы координат?
+ одна абсцисса и одна ордината
– одна абсцисса и ни одной ординаты
– ни одной абсциссы и одна ордината
– две абсциссы и две ординаты
8. Дана прямая, которая параллельна оси ординат. На ней взяты две точки F и K. У точки F абсцисса равна 7. Чему равна абсцисса точки K?
+ 7
– 0
– -7
– невозможно определить
9. На координатной плоскости отмечены две точки K и F. Определите координаты, соответствующие этим точкам.
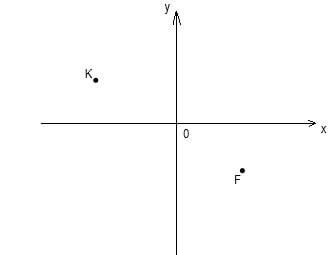
– K(x;y)F(x;-y)
+ K(-x;y)F(x;-y)
– K(-x;-y)F(x;-y)
– K(x;-y)F(x;y)
тест 10. На координатной плоскости изображен четырехугольник KTRS. Как называется этот четырехугольник, если координаты его точек равны: K(-1;3), T(6;3), R(4;-2) и S(-3;-2)?
– прямоугольник
– равнобедренная трапеция
+ параллелограмм
– квадрат
11. Как определить координаты середины отрезка на плоскости?
+ они равны полусуммам координат конечных точек отрезка
– они равны сумме координат конечных точек отрезка
– они равны половине произведения координат конечных точек отрезка
– они равны половине разностей координат конечных точек отрезка
12. Дан ромб SDFG. Необходимо найти координаты его вершины S, если координаты остальных вершин следующие D(-3;1), F(-1;4), G(1;1).
– S(-4;1)
– S(1;5)
+ S(-1;-2)
– S(4;-7)
13. Дан отрезок FG с точками F(2;6) и G(10;8). Найдите координаты точки K, если известно, что она является серединой отрезка FG.
+ K(6;7)
– K(4;1)
– K(10;24)
– K(-8;-2)
14. На рисунке изображен прямоугольный треугольник TKN с медианой NG. Найдите координаты точки G.
+ G(5;7)
– G(4;7)
– G(4;6)
– G(7;5)
15. Выберите, какая из предложенных величин является векторной?
– перемещение точки на плоскости
– сила
– скорость
+ все перечисленные
16. Дайте определение понятию «вектор»?
– это отрезок, который начинается в начале координат и имеет ненулевую длину
+ это отрезок, который имеет начальную и конечную точку, а также заданное направление
– это отрезок, который имеет численное значение, но не имеет направления
– это отрезок, который расположен в одной из четвертей прямоугольной системы координат
17. Верно ли утверждение, что любая точка на плоскости является вектором?
– да, но только в том случае, если этот вектор имеет определенное направление
– да, и его длина измеряется отрезком от начала координат до этой точки
+ да, и его длина равна нулю
– нет, утверждение не верно
18. Дан отрезок CD. Его длина называется длиной или … вектора , которая обозначается как . Вставьте пропущенное слово.
– расстоянием от точки C до точки D
+ модулем
– диаметром
– диагональю
19. Какое из утверждений верно для коллинеарных векторов?
– их длины отличны от нуля
– они находятся на параллельных или на одной прямой
– они могут быть направлены как в одном, так и в противоположных направлениях
+ все утверждения верны
тест-20. Какими бывают коллинеарные векторы:
+ сонаправленными и противоположно направленными
– параллельными и перпендикулярными
– соприкасающимися и разделенными
– направленными и точечными
21. Нулевой вектор коллинеарный… Продолжите утверждение:
– только сам с собой
– с вектором, проведенным из начала координат к точке нулевого вектора
+ сонаправленный с любым вектором
– противоположно направленный с любым вектором
22. В чем отличие равных векторов от противоположных?
+ у равных векторов одинаковое направление, а у противоположных – разное
– они имеют разные модули длины
– равные векторы расположены в одной четверти системы координат, а противоположные – в противоположных
– у них нет отличий
23. Выберите на рисунке с изображенным параллелограммом DFBN верную пару коллинеарных противоположно направленных векторов:
24. С помощью какой формулы определяются координаты вектора?
– через произведение координат точек конца и начала вектора
– через сумму координат точек конца и начала вектора
+ через разность координат точек конца и начала вектора
– через отношение координат точки конца к координатам точки начала вектора
25. Укажите верные координаты вектора
26. Определите координаты вектора , если известны координаты его начальной точки C(5;7) и конечной точки V(6;3).
– {1;-4}
+ {-1;4}
– {11;10}
– {10;-4}
27. Разложите вектор по двум координатным векторам
28. Длина вектора, который задан своими координатами равна:
– сумме квадратных корней из его координат
+ квадратному корню из суммы квадратов его координат
– произведению квадратных корней из его координат
– произведению его координат
29. Найдите длину вектора с координатами {-4;-3}.
– 7
– 25
– 12
+ 5
тест_30. На рисунке изображен прямоугольник RTYH, в котором длина вектора а длина вектора Найдите длину вектора
– 2 см
– 3 см
+ 2,5 см
– 4 см