Тесты – Треугольники 7 класс с ответами: бесплатные материалы для тестирования от преподавателя.
Тесты по геометрии 7 класс. Тема: “Треугольники”
Правильный вариант ответа отмечен знаком +
1. Найдите верное утверждение:
1) вершины треугольника лежат на одной прямой –
2) стороны треугольника параллельны друг другу –
3) для обозначения треугольников используют малые греческие буквы –
4) углы треугольников могут называться по их вершинам (∠A, ∠C) или по сторонам, которые их образуют (∠BAC) +
2. В прямоугольном треугольнике EBK проведены две биссектрисы – EM, BN. Чему равна градусная мера ∠BAE?

1) 45° –
2) 90° –
3) 120° –
4) 135° +
3. Стороны произвольного треугольника FNT относятся друг к другу как 6:7:11. Вычислите длину большей стороны треугольника, при условии, что его периметр равен 72 см.

1) 22 см –
2) 24 см –
3) 33 см +
4) 36 см –
4. Выберите вариант ответа, под которым расположена пара треугольников, равенство которых доказать нельзя:

1) 1 –
2) 2 +
3) 3 –
4) 4 –
5. Треугольник KEB – равнобедренный, в нём проведена медиана DK. ∠BKD=38°. Найдите градусную меру угла EKB.

1) 38° –
2) 45° –
3) 52° –
4) 76° +
6. Выберите, какие из треугольников не равны между собой на этом рисунке:

1) ΔCAB, ΔCDA –
2) ΔODA, ΔOBA –
3) ΔBOC, ΔBOA +
4) ΔCOD, ΔCOB –
7. Найдите неизвестный угол, исходя из данных на рисунке.

1) 75° –
2) 90° –
3) 105° +
4) 125° –
8. Вычислите, чему равен периметр равнобедренного треугольника MOD, если известно, что его основание OD в два раза больше боковой стороны.

1) 20 ед. –
2) 28 ед. +
3) 36 ед. –
4) 42 ед. –
9. Какое название имеет отрезок EK в данном треугольнике?

1) высота –
2) медиана –
3) биссектриса +
4) колено –
тест 10. В треугольнике ABC проведены три биссектрисы, которые пересекаются в точке O. ∠BAC=48°, ∠CBA=62°. Вычислите градусную меру угла AOC.

1) 35° –
2) 70° –
3) 110° –
4) 121° +
11. Выберите вариант ответа. Медиана проведена в треугольнике под номером:

1) 1 –
2) 2 +
3) 3 –
4) 4 –
12. На рисунке представлен прямоугольный треугольник. Сумма длин его гипотенузы и меньшего катета равна 24 см. Чему равна длина меньшего катета?

1) 4 см –
2) 6 см –
3) 8 см +
4) 12 см –
13. К основанию равнобедренного треугольника AKB проведена биссектриса AM. Необходимо вычислить длину стороны KA, если известно, что основание KB равно 8 см.

1) 2 см –
2) 4 см –
3) 8 см +
4) 12 см –
14. Какого признака равенства прямоугольных треугольников не существует?
1) по двум катетам –
2) по гипотенузе и острому углу –
3) по двум прямым углам +
4) по катету и прилежащему углу –
15. На рисунке представлен параллелограмм KMPN, состоящий из многих треугольников. ∠KMO=63°, ∠ONK=57°. Вычислите градусную меру угла PNK.

1) 63° –
2) 70° –
3) 120° +
4) 133° –
16. Треугольники ABD и CBD равнобедренные. ∠ABD=44°, AB=BC. Какова градусная мера угла CDA?

1) 44° –
2) 88° +
3) 90° –
4) 120° –
17. Какой признак можно использовать для доказательства равенства треугольников на рисунке?

1) первый –
2) второй +
3) третий –
4) они не равны –
18. В треугольнике DEO проведена медиана EN, равная 4 см. Определите периметр треугольника DNE, если периметр изначального треугольника DEO 19 см и OE=DO=8 см.
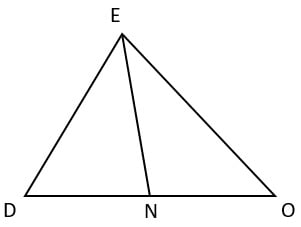
1) 7 см –
2) 8 см –
3) 9 см –
4) 10 см +
19. На рисунке представлена пара треугольников. Найдите, чему равен неизвестный угол.

1) 45° –
2) 55° +
3) 90° –
4) 135° –
тест-20. Найдите верное утверждение:
1) любой равносторонний треугольник является равнобедренным +
2) медиана и биссектриса совпадают в произвольных треугольниках –
3) длина основания равнобедренного треугольника всегда равна длине его боковой стороны –
4) в равностороннем треугольнике стороны равны высотам треугольника –
21. Треугольник CKB – равнобедренный, EC – высота, EC=8 см. Длина боковой стороны 10 см. Найдите длину основания KB.

1) 6 см –
2) 10 см –
3) 12 см +
4) 15 см –